What is a Finite State Transducer? Your first guess might be that its an essential component of a car-based time machine, like a flux capacitor. It isn’t, but believe it or not, we are going to travel back to 1955, have a chat with a George M, hopefully improve our lives in the present, and maybe even wrap a bulletproof vest around our code to protect it from unexpected disasters.
A Finite State Transducer is a Finite State Machine that also produces output. Well, that just defines it in terms of a Finite State Machine so let’s dig into that.
A Finite State Machine is a model of computation that focuses on the possible states that a system can be in and the possible transitions between them. At any given time, the system is sitting there happily in some state. Along comes a stimulus to the system, or an input. The system processes the input according to some rules. Maybe it doesn’t do anything in response to this input, and it’s in the same state it was. Maybe that input prompts some change and the system is in a new state. Nothing leaves the system in response to the input, but maybe outside observers can see the system’s current state at any time.
A vending machine is a classic example. It starts idle (state). You put some money in (input). It waits for you to push buttons to choose your item (state). You push the buttons (input). It dispenses your item and its back to idle (state).
A Finite State Transducer is that plus output. So you may be sending some information somewhere that could be useful to someone. An FSM is like a sink, things can go in, but nothing comes back out. An FST can emit things, which means you can integrate it into a larger system flow. In the vending machine, you might separate the controls from the dispensing machinery, and ‘dispense <item>’ might be an output from the controls FST to the dispenser.
Back to 1955…
There are different ways to model a system as an FST. One of those is the Mealy Machine. This model was pioneered by George Mealy and published in 1955 in his paper, “A Method for Synthesizing Sequential Circuits”.
Now, the Mealy Machine is perhaps too specific for our needs, but we needed it for our Back to the Future metaphor. We do want to grab one important thing here, which is the idea that the output values are determined by the current state and the current input. That gives us a transition function with this signature: (State, Input) => (State, Output). We’ll bring that back with us. Thanks George M.!
With that lightning-strike of genius, it’s time to leave the past.
Back to the future relative to 1955…
The FST is a model of computation that happens to fit well with many modern development patterns. We’ll take a look at how it relates to Event-driven Programming, Microservices, and the Actor Model.
From that transition function signature we brought back, we might illustrate an FST like this:
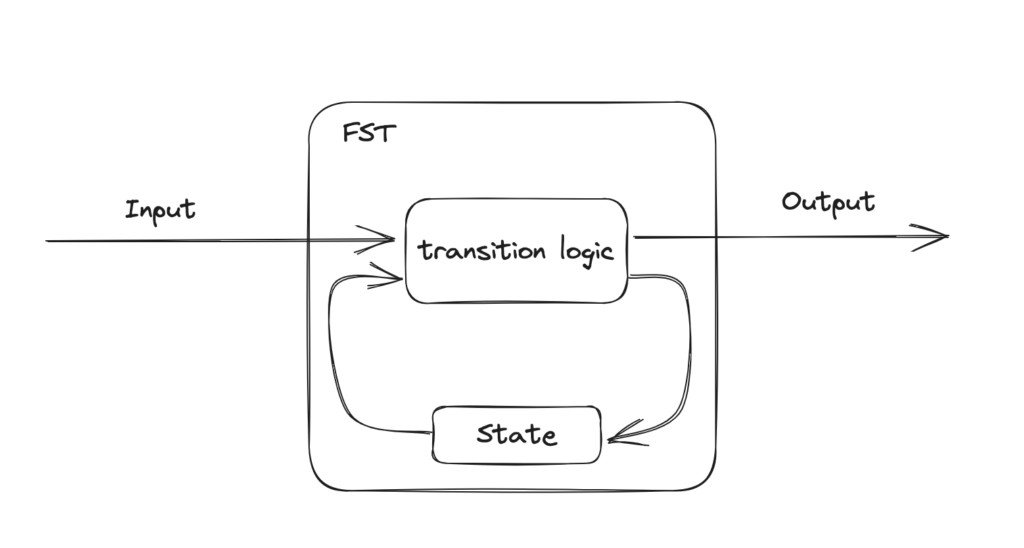
The FST is all about the inputs, outputs, possible states, and the declarative logic for how those things relate to each other. It is a fantastic tool for encapsulating logic within a broader system architecture.
Event-Driven and FSTs
Event-Driven is a broad term. For our purposes, we are going to focus on 3 components commonly found in such systems: Event Producer, Event Processor, and Event Consumer.
An Event Producer produces events. They are the source of input into the system. An Event Consumer consumes events. They take output out of the system. In between them sits one or more Event Processor nodes. They accept events from producers and send other events to consumers. We could illustrate that like this:
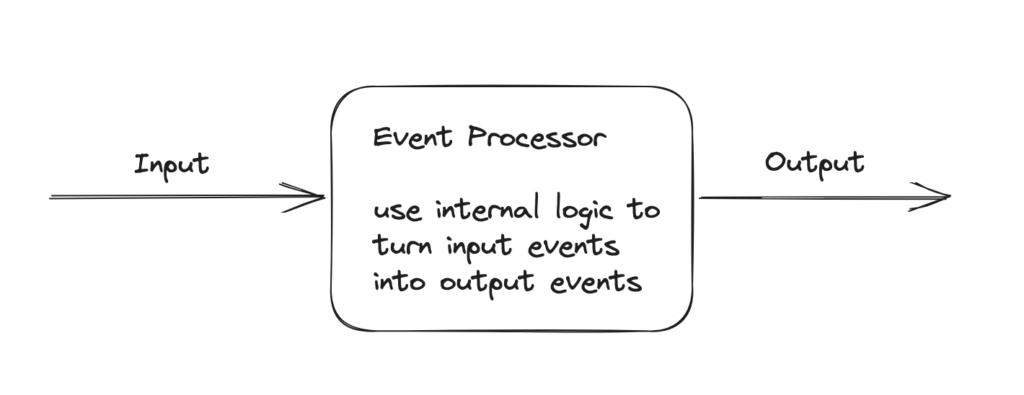
Looks a lot like the FST illustration, doesn’t it? An FST makes a great fit for an Event Processor.
Microservices and FSTs
We’ll specifically examine request/response services here. A client request comes in, we run some logic, and send a request back. We have an input (request), we may have some state, either in memory or in a database, and we have an output (response).
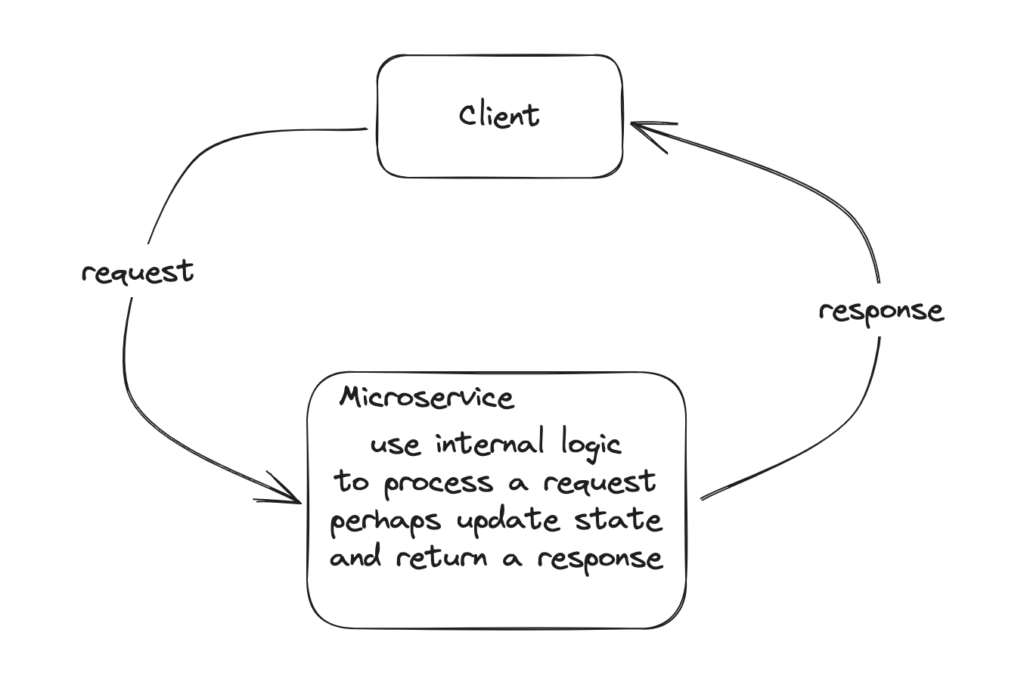
Pretty similar to an Event Processor. Another good fit for an FST.
Actor Models and FSTs
In an Actor Model, an Actor consists of a Mailbox, which is a queue of messages, a function to process a message, and some internal state. Actors may communicate with other actors by putting messages into their mailboxes. As an actor, messages in my mailbox are input, and messages I send to other actors are output.
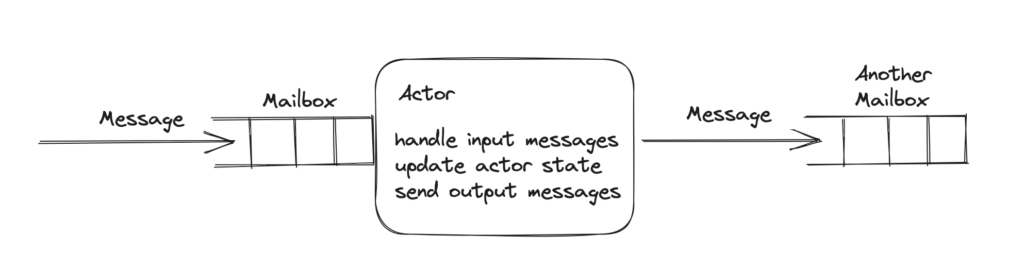
An FST is a great fit for the internals of an Actor, which can help separate the pure logic from the details of the actor system implementation.
How do we use this in code?
Like every other abstract model, there are many ways to implement an FST in code. The essential pieces are:
- A transition function, which accepts an input, uses the current state, updates the state, and produces an output.
- Storage of the state.
- A mechanism to submit inputs.
- A mechanism to receive outputs.
I broke an FST into those 4 parts because you may want to integrate them differently into different programming paradigms.
Remember what we brought back from 1955? The signature of an FST transition function is (State, Input) => (State, Output). That’s our starting point. For convenience, it may be preferable to produce more than one output element in a single transition, which would be (State, Input) => (State, Sequence<Output>). You may need your FST to work on mutable state, so you may actually use (State, Input) => Output. You may end up encapsulating your state inside the transition function or its owner, and use Input => Output.
In a Functional Programming environment, you may just want the transition function as a pure function. It just gets chained together with other functions. You might have something like this:
def transition(state: S, input: I): (S, O) = match (state, input) {
case (Idle, DoThing) => (Busy, FetchData)
case (Busy, GotData) => (Idle, PublishData)
case (_, _) => // invalid (state, input) pairs, log as error
}In an Object Oriented Programming environment, you may want to encapsulate the state inside an object, so perhaps you’ll create something like this:
interface FST<S,I,O> {
onInput(input: I): O
getState(): S
}
class ConcreteFst<S,I,O>(
initialState: S,
) implements Fst<S,I,O> {
private state: S = initialState
onInput(input: I): O {
// logic here to update the 'state'
// and return appropriate output
}
getState(): S {
// we can return actual state object
// or perhaps a copy or readonly version
return state;
}
}In a stream-based programming environment, you might have an asynchronous processing node like this:
interface FstNode<I, O> {
offer(input: I): void
listen(listener: (O) => void): void
}
// chain some nodes together...
source<I> -> myFstNode -> sink<O>Let’s wrap it up – FSTs and Precision?
Software Development is a modeling activity. We model an abstract or real-world process in a way that a computer can execute it. The FST is a model which forces us to focus on the possible valid states that process can be in, the possible user actions or events from other systems that we need to handle, and the events or requests we need to send to other systems. We are focused on the behaviors of the process and the interactions it has with other processes. When we are explicit about those things, it becomes easier to reason about the system and identify unhandled error situations that normally lead to bugs.
Consider a common situation of fetching data. A user might click a button which triggers an http call to get some data. A basic implementation might be to just put a click handler on the button that directly fetches the data. That might be fine. But what if its a big query that takes some time? And they click the button a bunch of times? Or if its a mutation action that should only be done once?
You can model that with an FST to precisely define what to do in different states.
// State, Input, Output are represented as sum types of different objects
type State = Idle | Fetching
type Input = Fetch | FetchDataSuccess | FetchDataFailure
type Output = SendFetchRequest | PublishData | ReportFetchingError | NilOutput
// pseudo-code
function transition(state: State, input: Input): (State, Output) {
match (state, input) {
case (Idle, Fetch) => (Fetching, SendFetchRequest)
case (Fetching, Fetch) => (Fetching, NilOutput)
case (Fetching, FetchDataSuccess) => (Idle, PublishData)
case (Fetching, FetchDataFailure) => (Idle, ReportFetchingError)
default:
// remaining cases should not happen
// we can log that as an error
}
}By feeding the input through the FST, you can now precisely control the conditions that cause an actual http request to be sent, and you can precisely define the error states which can help tremendously with production debugging.
This is a small, contrived example. Many processes are much more complex, and this level of precision becomes invaluable for avoiding bugs and identifying system failures. It also serves as clear communication of the details of the system to other team members or our future selves, which may be worth even more.
Diagrams made with Excalidraw